Bell’s Theorem – Does the moon exist when we are not looking at it?

Dear friends,

I have just spent a week at CERN, the world’s foremost research center for elementary particles. I was invited by a quantum physicist who had read my Psychology of Totalitarianism and who is providing thorough commentary on the physics chapters of my next book as I write them. I spent a week among particle accelerators, discussing from morning till night the nature of matter and the collapse of the wave function. One thing I know for certain now: nobody in the world knows what matter is. I actually knew that beforehand, but I am glad to know that physicists know they don’t know either.

In the week before I went to CERN, I immersed myself in the famous Bell’s theorem. The Irish physicist John Bell is, together with Peter Higgs, perhaps the best-known CERN researcher ever. His theorem is sometimes described as the most intelligent piece of science ever conceived. It is this theorem that ultimately addressed the question Einstein once mockingly put to Niels Bohr: “Do you really think the moon doesn’t exist when you’re not looking at it?”

On the internet you can find countless attempts to explain the theorem—some more successful than others. I have also made my own attempt to present the theorem in my own words. This explanation fits within a few chapters on physics in my new book. It is, at certain points, just a little too abstract to include in the book itself. That’s why I am posting it here.

My presentation approaches the mathematics behind the theorem in as accessible a way as possible. I would say: don’t be intimidated by a few formulas and symbols—invest a little energy in the fascinating story of Bell’s theorem.

..

At the beginning of the twentieth century, physics found itself in a tight spot. In 1802, Thomas Young had demonstrated through his famous double-slit experiment that light behaves like a wave. But in his miraculous year of 1905, Einstein had shown through his work on the photoelectric effect that light also behaves like a particle—at least under certain conditions. Both theories about light were logically coherent. Both were based on reproducible observations. But how can light be both a wave and a particle?

The rift between these two perspectives was bridged by a new theory: the now-famous quantum physics. Yet in many ways, quantum theory is a torment for common sense. It makes predictions that appear absurd—so absurd, in fact, that even Einstein, who laid the foundation for quantum mechanics through his work on the photoelectric effect, remained deeply skeptical of it.

Quantum theory claims, for example, that elementary particles — like all matter — do not exist in a definite state until they are observed. Before observation, they exist in a wave-like form that holds all possible properties at once — the so-called state of superposition. Einstein mocked this notion by asking Niels Bohr and his colleagues whether they truly believed the moon ceases to exist when we’re not looking at it.

Quantum theory also proposes the existence of “entangled” particles — particles that are identical at the level of their wave functions and therefore must share corresponding properties. In other words: the properties of one particle are inextricably linked to those of another.

This means that if you measure or manipulate one entangled particle, its twin — no matter how far away — instantly changes too. Since particles don’t assume definite properties until they’re observed, measuring one not only defines its own state, but also that of the other. So far, so good — or at least, so strange.

In the famous 1935 Einstein-Podolsky-Rosen paper, the authors argued that something was seriously wrong with quantum theory. If the theory is correct, then the change in one entangled particle causes an instantaneous change in the other — “instantaneous” meaning “without the passage of any time.” If true, this would imply that the information travels faster than light. And if that were the case, Einstein argued, such communication would be not material, but immaterial. “I do not believe in spooky action at a distance,” he sneered.

Einstein defended what’s known as “local realism.” Realism refers to the idea that particles exist independently of an observer. The entangled particles, once separated, may indeed respond to measurement or manipulation — but the way they respond depends on properties they already had, even if quantum theory doesn’t yet account for them.

Local, meanwhile, means that particles cannot be influenced by events happening far away if there’s no material interaction between them. In other words: quantum theory’s claim that distant particles react to each other faster than light is absurd.

Niels Bohr and the other quantum physicists stuck to their guns, though they admitted it would be extremely difficult — if not outright impossible — to prove their position through observation or experiment. Logically speaking, it seems impossible: how can you observe what properties a particle has before it’s been observed?

But nearly thirty years after Einstein’s critical paper, Irish physicist John Bell would demonstrate that the impossible might just be possible. In 1964, he published a short paper introducing what would become known as Bell’s Theorem — showing that an experiment could be devised to determine who was right: Einstein or Bohr.

**

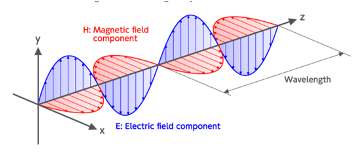
We begin with an introductory explanation of the polarization—or vibration direction—of light. This property of light is important for understanding our explanation of Bell’s theorem.

Light propagates (in wave form) as a transverse wave, meaning a wave whose vibration direction is perpendicular to the direction of propagation. Imagine a three-dimensional Cartesian coordinate system with orthogonal axes X, Y, and Z (see Figure 1). If the light wave moves in the direction of the Z-axis, then the wave oscillates perpendicular to Z—i.e., along a vector lying in the X-Y plane. The direction in which the wave vibrates is called the polarization of the light.

Light can consist of waves that all share the same polarization or have different vibration directions. The left part of Figure 1 illustrates this. There you see a beam of light traveling in a horizontal direction, made up of light waves oscillating in various directions perpendicular to that horizontal arrow. Some types of light, such as sunlight, exhibit all polarizations—that is, they contain waves oscillating in every possible direction within the X-Y plane

.

It’s important to note: while a light wave can consist of multiple polarizations, a single light particle or photon can only have one polarization. It vibrates in a single direction. It is the combination of many photons that allows a light wave or beam to exhibit multiple polarizations. This distinction will become important later, when we describe the experiment related to Bell’s theorem.

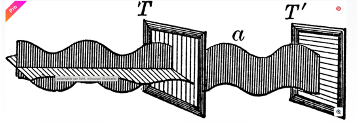
Light can be filtered using polarization filters (or polaroid filters), which allow only light with a specific polarization to pass through. This filtering results in a loss of light intensity. You might tentatively compare such a filter to a kind of blind or slatted screen (see Figure 2). These “slats” correspond to the so-called transmission axis of the polaroid filter, which is perpendicular to the hydrogen chains that make up the filter’s structure. When light waves strike the filter, they have a higher probability of passing through if their vibration direction aligns more closely with the direction of the slats.

Light waves that vibrate along a vector parallel to the slats will all pass through the filter. In that case, the angle between the polarization vector and the filter’s transmission axis is 0°, and the probability of transmission is 100%. In formula:

P(0°) = 100%

Light waves that vibrate in a direction perpendicular to the slats will all be blocked. In this case, the angle between the polarization vector and the transmission axis is 90°, so the probability of transmission is 0%. In formula:

P(90°) = 0%

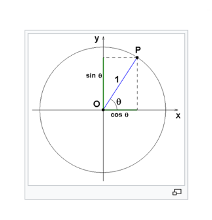
For light waves whose polarization vector forms an angle between 0° and 90° with the transmission axis, the probability of being blocked increases as the angle approaches 90°. You can calculate this probability using the sine squared of the angle X. A quick trigonometry refresher: the sine of an angle is simply the projection of the radius of a circle onto the vertical axis under that angle (see Figure 3).

It is immediately clear from this that the probability is highest at 0° and lowest at 90°. The general formula is:

P(X) = sin²(X)

When light with multiple polarizations strikes a polarizing filter, the filter will block (absorb or reflect) some of the light waves and allow others to pass through. The probability that a light wave passes through depends, as shown in the formula, on how closely the light’s polarization direction aligns with the transmission direction of the filter.

That concludes our short introduction to the physics of light. Now we move on to Bell’s theorem.

**

As mentioned earlier, Bell had devised something that allowed one to experimentally test whether entangled particles do or do not possess all their properties prior to observation, and whether or not they can “spookily” communicate with each other at a speed faster than light.

Imagine an experiment in which two entangled particles are emitted simultaneously and in opposite directions. In each direction, a scientist is waiting with three polarizing filters at their disposal:

• a filter A with a horizontal transmission axis,

• a filter B with a transmission axis tilted at 22.5° relative to the horizontal, and

• a filter C with a transmission axis tilted at 45° relative to the horizontal.

The two particles travel at the same speed (the speed of light), and the filters are placed at precisely equal distances from the source, so that both particles reach their respective filters at exactly the same time.

In the experiment, three series are carried out, each consisting of a large number of entangled particle pairs—let’s say a few hundred.

• The scientist who receives the first particle chooses to use filter A in the first series, again filter A in the second series, and filter C in the third series.

• The scientist who receives the second particle chooses to use filter B in the first series, filter C in the second, and again filter C in the third series.

This setup results in the following filter combinations for each entangled pair:

• Series 1: particle 1 meets filter A, particle 2 meets filter B

• Series 2: particle 1 meets filter A, particle 2 meets filter C

• Series 3: particle 1 meets filter C, particle 2 meets filter C

You may wonder why we are only considering these specific combinations of filters in the experiment. That is a good question. As you’ll soon see, the other combinations are indeed unnecessary.

At first glance, this experiment seems to make no progress at all in determining whether Einstein or Bohr was right. In fact, Einstein predicted exactly the same filter results as Bohr. According to both theories, the particles would either pass through certain filters or not, in the same way. The difference between Einstein’s and Bohr’s theories lies entirely in the explanation of the particles’ behavior—not in the behavior itself.

Einstein believed that the particles already “knew” in advance whether they would pass through a given filter or not—simply because all their properties were already determined beforehand. Bohr, on the other hand, believed that—for reasons beyond our reach—the particles made that choice at the moment of measurement, and only then acquired the properties that would determine whether they would pass or not.

In a flash of genius, Bell realized that Einstein’s and Bohr’s theories actually do make different predictions. The statistical probability that entangled light particles pass through the filter differs depending on whether the calculation is based on the assumption that Einstein’s theory (i.e., local realism) is correct, or whether it is based on the assumption that Bohr’s theory (i.e., quantum theory) is correct.

We will now go ahead and perform the calculation of both probabilities.

**

If Einstein is right, then the particles already possess the properties in advance that will determine whether or not they pass through the filter. We don’t know those properties—they are hidden variables—but they are definitely already there beforehand. That’s simply the reasoning that our common sense provides. Reality and matter exist, whether we are looking at them or not.

Bell realized that in this case, you cannot precisely calculate the probability that the particles will or won’t pass through the filter (since you don’t know the relevant properties in advance), but you can determine a ratio or inequality in the probability distributions across the three conditions (i.e., the three series of particle pairs fired) of the experiment, based on simple logic.

We use the following symbols in laying out that logic:

• P = Probability

• A = the passsing of a particle through filter A

• Ā= the NOT passsing of a particle through filter A

• B = the passing of a particle through filter B

• Ḃ = the NOT passing of a particle through filter B

• C = the passing of a particle through filter C

• Ċ= the NOT passing of a particle through filter C

Here we go.

If Einstein is right and the properties of the elementary particles are fixed in advance, then it is also fixed in advance whether a particle will or will not pass through filter A, B, or C. Based on the following simple (algebraic) logic, we can then say something about the probability that a particle has the potential to pass through combinations of filters A, B, and C:

(1) P(AB̄) ≥ P(AB̄C̄)

According to our notation, we read this as:“The probability that a particle passes through filter A and not through filter B is greater than or equal to the probability that it passes through filter A and not through filter B and not through filter C.”

There’s no arguing with that—it is as logically sound as anything can be.

In the same way, we arrive at the following expressions:

(2) P(BC̄) ≥ P(ABC̄)
(3) P(AC̄) = P(AB̄C̄) + P(ABC̄)

From the combination of (1), (2), and (3), we can very simply derive:

(4) P(AC̄) ≤ P(AB̄) + P(BC̄)

In this way, Bell determined a specific inequality between the probabilities that a particle would or would not pass through certain combinations of filters.

**

We can now determine exactly the same probabilities under the condition that it is not Einstein but rather Bohr (i.e., quantum mechanics) who is right. For this, he used a different kind of calculation.

Quantum mechanics assumes that a particle only acquires its properties at the moment those properties are registered or measured. For example, the polarization direction of a particle can “come into being” as it passes through a filter and is thereby “measured.” That is precisely what we do in the experiment described here: we send particles through a filter and thereby determine their polarization.

Since, according to Bohr, the particle has no polarization before passing through the filter, it always has a 50% chance of passing through any filter.

It is precisely at this point that the difference between Einstein’s theory and Bohr’s theory becomes relevant. According to Einstein, each particle has an unknown but definite chance of passing a filter, depending on its pre-existing, hidden properties. According to Bohr, each particle has exactly a 50% chance (½) of passing through any filter.

At the moment the particle passes through the first filter, its polarization direction becomes fixed/materialized, and from that point on, there is a definite probability that it can pass through another filter.

Let us note here: in our experiment, the two particles pass through their respective filters at exactly the same time. Is that a problem? No. We can arbitrarily designate one of the two filters as the “first,” and the rest of the reasoning proceeds accordingly.

So: the probability that the particle passes the first filter is always 50%. The probability that it passes the second filter depends on the difference in angle between the transmission axes of the two filters. As we showed earlier, we can calculate that probability by squaring the sine of that angle.

Using this, we can calculate each of the probabilities that appear in the inequality we derived earlier under the assumption that Einstein was right.

We first calculate the probability that a particle passes through filter A but not through filter C. The angle between the transmission axes of filters A and C is 45° (see earlier). The formula to calculate the probability that a particle passes A but not C is:

(1) P(AC̄) = 50% * sin²(45°) = 50% * 0.500 = 25%

If we apply the same formula to the two other relevant probabilities, we get:

(2) P(AB̄) = 50% * sin²(22.5°) = 50% * 0.146 = 7.3%
(3) P(BC̄) = 50% * sin²(22.5°) = 50% * 0.146 = 7.3%

Now comes the key point. If we fill in these values in the probability inequality that we derived under the assumption that Einstein was right, we see that they are incompatible. Let’s do that.

Under the condition that Einstein was right, we found the following inequality (see earlier):

  P(AC̄) < P(AB̄) + P(BC̄)

If we now substitute the values we calculated under the assumption that Bohr was right, we get:

  25% < 7.3% + 7.3%

Which is clearly false.

In other words: Bell’s theorem shows that—contrary to the initial impression—Einstein’s and Bohr’s theories do not predict the same outcomes, and that an experiment can, in fact, determine which one of the two was right.

**

At that time, the equipment required to carry out the experiment was not yet sufficiently advanced. It wasn’t until 1982 that this became the case. Alain Aspect then tested Bell’s theorem, and the outcome left no room for doubt: Einstein was wrong, Bohr was right.

The consequences for our view of reality are enormous. The test of Bell’s theorem showed that elementary particles are wave patterns in a state of superposition before being observed, and that they communicate with each other ‘timelessly’ over any distance. Since these elementary particles are the building blocks of our entire reality, this implies that our entire reality is in superposition as long as it is not observed. What is true for each tiny brick of a house is, in a sense, also true for the house itself.

Einstein once sneered at Bohr: “Do you really believe that the moon ceases to exist if you’re not looking at it?”
We can now answer him: Indeed. Or at least: it does not exist in the way it exists when we are looking at it. Man is a co-creator of the reality in which he lives; he does not passively undergo it.

But what exactly causes the wave in superposition to become a particle? Is it the act of measuring, or the act of observing?
The most conservative stance is to claim that it is the material measuring apparatus that changes what is being observed. In that case, one still clings—if only with one hand—tightly to the branches of the materialist trees. Most academic physicists probably opt for this position.

But then I wonder: Einstein wasn’t referring to the material act of measuring when he mentioned the moon; he was talking about looking at the moon. He clearly interpreted quantum theory as a theory that believes it is the act of looking that is decisive (even without measuring equipment).
Likewise, I wonder: we do not see the world around us as a wave in superposition, but as a collection of particles with more or less fixed properties.
Does this not imply that the act of looking itself caused the wave function to collapse, and that the particle became a fixed particle?
To paraphrase Einstein: Do we really believe that the collapse of the wave function does not occur if there are no physicists measuring particles?

Finally: in the many variations of the double-slit experiment, it turns out that a wave becomes a particle precisely at the moment the camera that registers it actually makes an unambiguous registration.
For instance, if electrons are fired at the double slits and we register the exact position of the electron with a camera using light frequencies, then it is observed that exactly at the moment the light frequency becomes high enough to register the electron, the wave pattern collapses and the electron becomes a particle.

These experimental findings also suggest, in my opinion, that what is decisive is not the material measuring apparatus itself—which remains the same, regardless of the light frequency—but rather the act of registering or observing itself.
In other words: it is the ‘act of consciousness’ in observation that is decisive.

Lastly, it is the case that the founders of quantum theory, based on their theory and their observations, declared the materialist worldview to be incorrect, and leaned toward a mystical or idealist worldview, in which consciousness is regarded as the cause of matter (and not the other way around, as materialism claims).

And if we see how even someone as admirable as Niels Bohr vacillated somewhat on this theme—sometimes warm, sometimes cold—then perhaps we must ultimately conclude that even the greatest among us did not entirely overcome a certain fear of the (materialist) masses.

Mattias